La curva de Laffer es uno de los conceptos económicos más citados y a la vez más malinterpretados del debate fiscal contemporáneo. Desde su introducción popular por Arthur Laffer en la década de 1970, se ha utilizado para justificar recortes de impuestos bajo la promesa de mayores ingresos fiscales. Pero, ¿qué dice realmente esta curva? ¿Cuáles son sus fundamentos teóricos? Y más importante: ¿cuál es su validez empírica y relevancia política hoy en día?
1. Qué es la Curva de Laffer
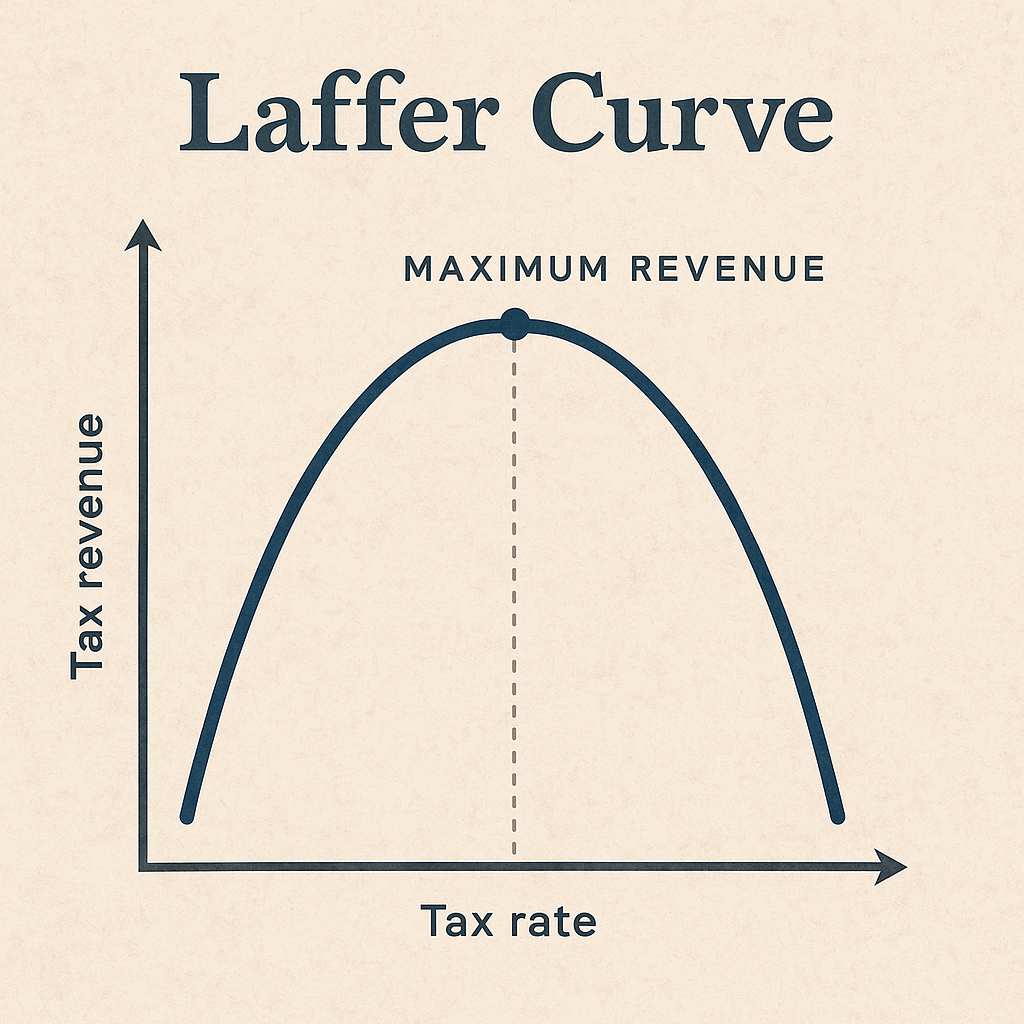
La curva de Laffer describe una relación hipotética entre el nivel de los impuestos y los ingresos fiscales que obtiene el Estado. Parte de dos puntos extremos: si la tasa impositiva es 0%, el Estado no recauda nada; si es 100%, los incentivos para trabajar o invertir desaparecen por completo y la recaudación también cae a cero. Por tanto, debe existir un punto intermedio en el que la recaudación es máxima.
Esto implica que, a partir de cierto nivel de impuestos, aumentarlos más podría reducir la recaudación, ya sea por disminución de la actividad económica, migración de capitales, reducción del esfuerzo laboral o aumento de la evasión fiscal.
2. Fundamentos Teóricos y Críticas
La base microeconómica de la curva de Laffer parte de la teoría de la oferta: a mayor carga impositiva, menor incentivo a trabajar, invertir o declarar ingresos. El impacto exacto depende de la elasticidad de la base imponible con respecto a la tasa impositiva. Es decir, cuánto se contrae la base gravada cuando aumenta la tasa.
Modelos teóricos como el de Mirrlees (1971) y las contribuciones posteriores de Saez (2001) han intentado optimizar la tributación bajo estas restricciones. En ellos, se muestra que un sistema fiscal óptimo debe balancear la eficiencia (minimizar distorsiones) con la equidad (redistribución del ingreso). Sin embargo, estos modelos son sensibles a supuestos sobre preferencias individuales, información asimétrica y mercados incompletos.
Las principales críticas a la curva de Laffer son:
- Simplicidad excesiva: No considera el tipo de impuesto (ingreso, consumo, corporativo), ni su estructura progresiva.
- Desconexión empírica: Rara vez los países están en la parte descendente de la curva.
- Instrumentalización política: A menudo se usa para justificar reducciones de impuestos sin evidencia robusta del efecto sobre ingresos.
3. Evidencia Empírica
Estimar empíricamente la curva de Laffer implica medir la elasticidad de la base imponible. Una revisión clásica de Saez, Slemrod y Giertz (2012) encuentra que para países como EE.UU., la elasticidad del ingreso gravable respecto a tasas marginales es moderada (alrededor de 0.2 a 0.4), lo que sugiere que hay espacio para subir tasas sin perder recaudación.
En el Reino Unido, un estudio de HMRC (2012) sobre la reducción de la tasa máxima del impuesto al ingreso del 50% al 45% concluyó que la pérdida de recaudación fue significativa y no compensada por aumentos en la actividad económica. En Francia, la «tasa del 75%» a los ingresos altos (2013–2015) fue eliminada sin haber causado una caída dramática de la base imponible, aunque sí incentivó algunas estrategias de elusión fiscal.
Por contraste, en países con sistemas poco eficaces de fiscalización, tasas marginales elevadas sí pueden erosionar la base gravable rápidamente, por lo que el contexto institucional es crucial.
4. Relevancia Política Actual: El Caso Trump 2025
En su propuesta de segundo mandato, Donald Trump ha sugerido extender e incluso profundizar los recortes fiscales establecidos por la Ley de Recortes de Impuestos y Empleos de 2017 (TCJA). La justificación sigue una lógica implícita en la curva de Laffer: que menores tasas generarán mayor crecimiento económico, inversión y, eventualmente, mayores ingresos fiscales.
Sin embargo, evaluaciones del Congressional Budget Office (CBO) y del Tax Policy Center indican que la TCJA no se autofinanció. Aunque hubo cierto estímulo de corto plazo, el déficit fiscal aumentó y los beneficios se concentraron en los deciles más altos. La curva de Laffer fue citada retóricamente, pero la evidencia mostró límites a su aplicabilidad en el contexto estadounidense actual.
Esto refuerza la necesidad de distinguir entre el uso político y el valor analítico de la curva. Más que un argumento para bajar impuestos, debería ser una invitación a diseñarlos con inteligencia, considerando efectos conductuales, progresividad y eficiencia recaudatoria.
5. Implicaciones para México
Aplicar la lógica de la curva de Laffer en México enfrenta retos estructurales significativos. En primer lugar, la informalidad laboral supera el 55% de la población ocupada, lo que limita la base imponible efectiva. En segundo lugar, la recaudación fiscal es de las más bajas de América Latina (alrededor del 16-17% del PIB), muy por debajo del promedio de la OCDE.
Además, la desigualdad y pobreza estructural generan presiones sociales para una política fiscal progresiva, más orientada a la redistribución que a la pura eficiencia. La elasticidad de la base gravable es baja en muchos sectores, pero también lo es la capacidad administrativa para vigilar, fiscalizar y reducir la evasión.
Recortes de impuestos en este contexto no solo tendrían un impacto fiscal limitado, sino que podrían agravar la dependencia de ingresos petroleros o de financiamiento externo. En cambio, una reforma que combine ampliación de la base (formalización, digitalización) con mejor progresividad y eficiencia del gasto tendría más potencial para aumentar la recaudación sin caer en los extremos de la curva de Laffer.
Conclusión
La curva de Laffer no es una receta universal para bajar impuestos, sino una herramienta que debe usarse con cuidado y contexto. Su valor real está en recordarnos que los impuestos sí afectan el comportamiento económico, pero sus efectos dependen de estructuras institucionales, grado de informalidad, elasticidad de la base y objetivos de equidad.
En economías como la mexicana, más que buscar el punto óptimo de la curva, es prioritario fortalecer la capacidad recaudatoria, cerrar brechas y construir un sistema fiscal progresivo, transparente y sostenible. Las decisiones fiscales no se toman en el vacío: tienen consecuencias sociales y políticas profundas.
¿Qué opinas sobre la validez de la curva de Laffer en tu país? ¿Crees que los recortes fiscales actuales están justificados? ¡Comparte tu punto de vista en los comentarios o en nuestras redes sociales!
Fuentes
- Mankiw, N. G. (2020). Principles of Economics. Cengage Learning.
- Saez, E., Slemrod, J., & Giertz, S. H. (2012). «The Elasticity of Taxable Income with Respect to Marginal Tax Rates: A Critical Review». Journal of Economic Literature.
- OECD. (2011). Tax Policy Reform and Economic Growth.
- IMF. (2013). Taxing Times. Fiscal Monitor.
- HMRC. (2012). «The Exchequer effect of the 50 per cent additional rate of income tax».
- Tax Policy Center. (2018). «Did the TCJA Pay for Itself?» Brief.
- CEPAL. (2023). Estadísticas Tributarias en América Latina y el Caribe.
Anexo: Desarrollo Matemático de la Curva de Laffer
Supongamos que la recaudación fiscal RR es función de la tasa impositiva tt y de la base imponible B(t)B(t), es decir: R(t)=t⋅B(t)R(t) = t \cdot B(t)
Se supone que la base imponible disminuye con tt, es decir, B′(t)<0B'(t) < 0. Para encontrar el punto de recaudación máxima, derivamos: R′(t)=B(t)+t⋅B′(t)R'(t) = B(t) + t \cdot B'(t)
La condición de máximo es cuando R′(t)=0R'(t) = 0, es decir: B(t)+t⋅B′(t)=0B(t) + t \cdot B'(t) = 0
Esta condición permite resolver para la tasa t∗t^* que maximiza los ingresos fiscales. Sin embargo, cada forma implica un distinto grado de sensibilidad de la actividad económica a los impuestos y, por tanto, un «pico» diferente de la curva de Laffer.
Deja un comentario